tl;dr

회귀분석을 선형 대수를 통해서 이해하면 새로운 깨달음을 얻을 수 있다.
회귀분석이라는 것은 PCA와 마찬가지로 차원을 '축소’하는 방법이다. $n$ 개의 관찰을 지닌 어떤 대상을 이보다 낮은 $k(<n)$ 개의 변수로 요약하는 것이 핵심이다.
선형대수로 보면 $\mathrm R^2$ 은 피타고라스 정리의 흔한 응용 사례에 불과하다.

공간에서 바라본 회귀분석

여기서 회귀분석을 해설할 생각은 없다. 이미 너무나 많은 그리고 매우 훌륭한 내용들이 책, 웹, 강의로 넘쳐날테니까. 이 글의 용도는 그림 하나로 지나치기 쉬운 회귀분석의 '핵심’을 살피는 것이다. crossvalidated에서 위 그림을 보는 순간 일종의 '돈오돈수’가 강림했다. (이렇게 이해하면 쉬웠을 것을…) 먼저 우리에게 익숙한 회귀분석 모델을 매트릭스로 적어보자.

$\underset{n \times 1}{\phantom{\bm \gamma}\mathbf{Y}\phantom{\bm \gamma}} = \underset{n \times k}{\phantom{\bm \gamma} \mathbf{X} \phantom{\bm \gamma} }\underset{k \times 1}{\bm \beta} + \underset{n \times 1}{\phantom{\bm \beta} \bm \varepsilon \phantom{\bm \gamma} }$

식에 관한 자세한 설명 역시 생략한다. 대충 $n$ 개의 관찰 수과 $k$ 개의 regressor를 지닌 중회귀분석 모형이라고 생각하면 되겠다. 앞서 본 그림은 보통 회귀분석의 예시로 많이 활용되는 아래 그림과는 다르다.¹

위 그림은 1개의 regressor가 존재할 때 이것과 regressand를 그대로 2차원 평면에 관찰 수만큼 찍은 것이다. 첫번째 그림에서 "Observed Y"는 점 하나가 $n$ 개의 regressand를 모두 포괄한다. $\mathbf{Y} \in {\mathbb R}^{n}$ 벡터, 즉 $n$ 차원 벡터이고, 이것이 회귀식 좌변의 관찰값 $n$ 개를 표현한다.

이제 선형대수의 세계로 들어가보자. $\mathbf X$ 의 열(column)이 각각 $n$ 개의 관찰 값을 지닌 regressor에 해당한다. 이 각각의 컬럼 $x_i$ 는 $x_i \in {\mathbb R}^{n}$ 벡터이다. $x_i$ 벡터 $k$ 개가 생성할 수 있는 공간이 $\mathbf X$ 의 열 공간(column space)이다. 앞으로 이를 col $\mathbf X$ 로 표기하자.

이렇게 생각하면 좋겠다. $x_i \in {\mathbb R}^{n}$ 벡터가 $k(<n)$ 개 있다고 하자. 이는 $n$ 보다 차원이 낮기 때문에 기하학적으로는 $n$ 차원 공간에서 초평면(hyperplane)으로 나타날 것이다. 위 그림에서 컬럼 스페이스가 평면으로 표현되는 것은 이러한 취지다. 3차원 벡터의 열 공간이 생성하는 초평면을 예시하면 아래와 같다.

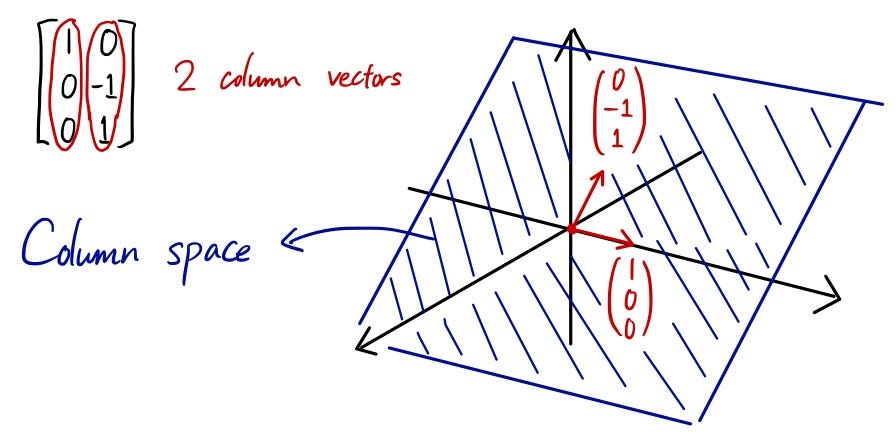
col $\mathbf X$ 의 최대 차원, 즉 $\mathbf X$ 의 랭크(위수)는 무엇일까? 회귀분석에서는 대체로 $n > k$ 가 일반적이고 이런 상황에서 $\mathbf X$ 의 랭크는 $k$ 를 넘을 수 없다. 다시 말하면, $\mathbf X$ 가 생성하는(span)하는 컬럼 스페이스의 차원의 크기가 $k$ 를 넘을 수 없다. 그리고 잘 된 회귀분석이라면 ${\rm rank}(\mathbf X) = k$ 를 만족한다.

맨 앞에 제시했던 그림을 다시 보자. 아래 색칠된 평면이 $\mathbf X$ 가 생성하는 컬럼 스페이스, 즉 col $\mathbf X$ 를 표현하고 있다. 몹시 특별한 경우가 아니라면 $\mathbf Y \in {\mathbb R}^{n}$ 벡터가 col $\mathbf X$ 에 속할 가능성은 없다. 그렇다면 회귀분석의 필요도 애초에 없었을 것이다. col $\mathbf X$ 를 통해서 $\mathbf Y$ 를 완벽하게 예측할 수 있는데 무슨 걱정이 있겠는가? 대체로 우리가 마주하는 상황은 $n$ 차원 벡터를 $k$ 차원 공간에 끼워 넣기 힘든 상황이다.²

회귀분석의 목표는 regressor를 통해서, 더 정확하게는 regressor의 집합이 생성하는 공간을 통해서 regressand를 ‘가장’ 잘 설명하는 것이다. 회귀분석이란 regressand와 ‘닮은’ 것 col $\mathbf X$ 에서 찾는 것이다. 즉 $\mathbf Y$ 와 닮은 무엇을 $\mathbf X$ 의 컬럼 스페이스에 찾아야 한다. 직관적으로 쉽게 떠올릴 수 있는 것은 이 평면과 $\mathbf Y$ 의 (유클리드) 거리를 가장 짧게 만들어주는 벡터일 것이다. 그리고 이 최단거리는 $\mathbf Y$ 에서 $\mathbf X$ 컬럼 스페이스로 내린 수선의 발이 닿는 col $\mathbf X$ 의 지점이다. col $\mathbf X$ 내에 있는 이런 지점을 찾는 연산자(operator)가 회귀분석 계수 $\hat{\bm \beta}$ 이다. 즉,

$\hat{\bm \beta} = ({\mathbf X}'{\mathbf X})^{-1} ({\mathbf X}' \mathbf Y)$

그리고 이 연산자를 reggressor의 모음인 col $\mathbf X$ 에 적용하면, $\mathbf{X} \hat{\bm \beta} =\hat{\mathbf Y}$ 이 계산된다. 그림에서 보듯이 $\hat{\mathbf Y}$ 은 $\mathbf Y$ 와 col $\mathbf X$ 의 거리를 최소화하는 위치에 존재한다. $\hat{\mathbf Y}$ 는 어떤 벡터일까? $\hat{\mathbf Y} \in {\mathbb R}^n$ 벡터지만, col $\mathbf X(\in {\mathbb R}^k)$ 내에 위치하고 있다. $n$ 차원이 $k$ 차원으로 축소된 셈이다. 이것이 회귀분석의 핵심이다.

선형 대수의 관점에서 내용을 다시 음미해보자. $x_i \in {\mathbb R}^n$ (for $i = 1, \dotsc, k$ ) 벡터의 리그레서 $k$ 개를 선형 결합해서 초평면의 한점, 즉 원래의 관찰 $y$ 와 최소 거리를 지니는 벡터를 찾아야 한다. 이 거리를 최소화하는 $\beta_i$ 를 알고 있다면 이 벡터는 다음과 같이 표현된다. ${\mathbf X} = [x_1, \dotsc, x_k]$ 일 때,

$\begin{aligned} \underset{(n \times 1)}{\hat{\mathbf Y}} & = X\beta \\ & = [x_1, \dotsc, x_k] \begin{bmatrix} \beta_1 \\ \vdots \\ \beta_k \end{bmatrix} \\ &= x_1 \beta_1 + \dotsc + x_k \beta_k \end{aligned}$

아래 그림을 참고하자.

이제 $\mathrm R^2$ 의 의미를 살펴보자. 결론부터 이야기하면 $\mathrm R^2$ 는 그림에서 $(\mathbf Y - \overline{\mathbf Y})$ 벡터와 $(\hat{\mathbf Y}-\overline{\mathbf Y})$ 벡터가 이루는 각의 코사인 값, 즉 $\cos \theta$ 다.

$\overline{\mathbf Y}$ 는 무엇일까? 포스팅의 맨 처음 보았던 그림과 같이 $\overline{Y} \mathbf{1}_n$ 로 표기할 수 있다. $\mathbf Y$ 의 평균값 $\overline{Y}$ 만으로 구성된 $(n \times 1)$ 벡터다. 이 벡터는 col $\mathbf X$ 안에 있을까? 당연히 그렇다. $\mathbf X$ 는 최대한 $k(<n)$ 차원의 벡터이고, $\overline{\mathbf Y}$ 는 1차원 벡터다.³

어쨌든 이 코사인 값의 의미는 무엇일까?

그림에서 보듯이 세 개의 벡터가 직각삼각형을 이루고 있으므로 아래의 식이 성립한다.

$\underset{\text{TSS}}{\Vert \mathbf Y - \overline{\mathbf Y} \Vert^2} = \underset{\text{RSS}}{\Vert \mathbf Y - \hat{\mathbf Y} \Vert^2} + \underset{\text{ESS}}{\Vert \hat{\mathbf Y} - \overline{\mathbf Y} \Vert^2}$

흔한 피타고라스의 정리다. 그런데 이것 어디서 많이 보던 식이다. 회귀분석 배우면 언제나 나오는 식이다. Regressand의 평균과 관찰의 이른바 총 제곱의 합(TSS: Total Sum of Squares)은 설명된 제곱의 합(ESS: Explained Sum of Squares)과 잔차 제곱의 합(RSS:Residual Sum of Squares)와 같다. 대체로 복잡하게 소개되는 이 식이 기하학적으로 보면 그냥 피타고라스의 공식에 불과한 것이다.

양변을 $\Vert \mathbf Y - \overline{\mathbf Y} \Vert^2$ 으로 나누면 다음과 같다.

$1 = \dfrac{\Vert \mathbf Y - \hat{\mathbf Y} \Vert^2}{\Vert \mathbf Y - \overline{\mathbf Y} \Vert^2} + \dfrac{\Vert \hat{\mathbf Y} - \overline{\mathbf Y} \Vert^2}{\Vert \mathbf Y - \overline{\mathbf Y} \Vert^2}$

정의에 따라서 $1 = \dfrac{\text{RSS}} {\text{TSS}} + {\mathrm R}^2$ 가 된다. 즉,

${\mathrm R}^2 = 1 - \dfrac{\text{RSS}}{\text{TSS}}$

사실 $\textrm R^2$ 는 가끔 회귀분석의 성과 지표로 남용되는 경우가 있다. 이렇게 기하학적으로 보면 col $\mathbf X$ 내에 표현된 $\hat{\mathbf Y}$ 가 $\mathbf Y$ 와 얼마나 가깝게 있는지를 $\overline{\mathbf Y}$ 를 기준으로 지표화한 것에 불과하다.

${\mathrm R}^2$ 는 회귀분석의 성과 지표로 어떤 의미가 있을까? 분석의 목표가 회귀분석을 통한 예측이라면, 즉 원래 관찰값과 예측된 값이 얼마나 떨어져 있는지 여부가 중요하다면 $\textrm R^2$ 는 의미를 지닐 수 있다. 반면, 분석의 목표가 회귀분석을 통한 이러한 종류의 예측이 아니라 특정한 regressor의 인과관계에 관한 추정이라면, $\textrm R^2$ 는 거의 무시해도 좋다.

아울러 회귀분석이라는 이름을 달고 있지만 전형적인 회귀분석의 방법을 따르지 않는 기법에서 $\textrm R^2$ 가 정의되지 않는 경우도 있다. 잘 알려진 로지스틱 회귀가 이에 해당한다. 로지스틱 회귀에서 회귀 계수의 추정은 여기서 봤듯이 관찰과 col $\mathbf X$ 사이의 거리를 최소화하는 방식이 아니라 우도(likelihood)를 극대화하는 방식을 따른다. 따라서 벡터 공간의 피타고라스 정리를 따르는 $\textrm R^2$ 는 정의되지 않는다.⁴

덤: 회귀 분석과 PCA는 서로 얼마나 다를까?

회귀 분석과 PCA는 어떻게 다른가? 여러가지 답이 있을 수 있다. 그걸 다 소개하겠다는 게 아니다. 둘이 데이터 모델링의 시야에서 어떻게 다른지를 살펴보는 게 이 글의 목적이다.⁵ 이 글은 둘을 어떻게 실행하는지를 다루지 않는다. 앞선 PCA 관련 포스팅을 읽고 오시면 이해에 도움이 될 것이다.

공통점

Feature

일단 둘 다 $k$ 개의 feature 비슷한 것을 지닌다. 그리고 $n$ 개의 데이터 포인트가 제시된다.

차원 축소

흔히 PCA를 차원축소의 방법으로 이해하는데, 이 말은 맞다. 반대로 회귀분석은 이와 다르다고 이해하는 경우가 많은데 이 말은 틀리다. 회귀 분석도 어떻게 보면 '차원 축소’다. 회귀 분석에서 target 변수는 $n$ 차원 공간 위의 주어진 한 점이다. 우리의 목표는 이 한 점을 잘 설명하는 더 낮은 차원의 어떤 지점을 찾는 것이다. 이런 점에서 본다면 회귀 분석 역시 차원 축소의 한 방법이라고 봐야 할 것이다.

극소화

PCA에서 '분산 최대화’에 이르기까지 과정을 생략하다보면, PCA를 별도의 어떤 방법으로 인식하곤 한다. 그런데 앞선 포스팅에서 보았듯이 '분산 최대화’란 사실 피처 벡터와 이를 예측하기 위한 어떤 벡터 사이의 거리를 최소화하는 과정에서 도출된 결과다. 이런 점에서 본다면, 회귀 분석이든 PCA는 MSE(Mean Square Error)를 최소화한다는 점에서는 목적 함수의 유형은 동일하다.

차이점

Supervised or Unsupervised?

회귀 분석과 PCA를 지도 학습(supervised learning), 비지도 학습(unsupervised learning)으로 구분할 수는 없다. 다만 이 구분과 어느 정도 비슷한 부분이 있다. 회귀 분석은 target이 있다. 이 타겟과의 거리를 최소화하는 feature 공간의 어떤 위치를 찾는 것이 목적이다. 반면, PCA에는 target이 없다. $k$ 개의 feature를 최소 거리로 투영할 수 있는 스크린 벡터를 찾는게 목적이다. 간단히 말해서 PCA는 target 없이 벡터의 거리가 1인 임의의 프로젝션 벡터를 찾는 것이 목적이다.

Jun Sok Huhh | 🏠lostineconomics.com

흔히 $\mathbf Y$ 를 종속변수, $\mathbf X$ 를 독립변수로 부르기도 한다. 하지만 이러한 이름에는 혼란의 여지가 있다. 여기서는 regressor, regressand라는 영어 표현을 그대로 쓰도록 하겠다. ↩︎
이를 선형 대수에서 배운 연립방정식을 푸는 문제로 이해해도 좋겠다. $A x = b(b \neq \boldsymbol{0})$ 라고 하자. $n$ 개의 미지수가 유일한 해를 지니고 위해서는 ${\rm rank}(A) = n$ 이어야 한다. 즉 서로 독립인 식이 $n$ 개 주어져야 고유의 해 $x$ 를 찾을 수 있다. 그런데 회귀분석은 식이 $k(<n)$ 개만 주어진 상황이다. ↩︎
왜 그런지 잠시 따져보자. 앞서 보았듯이 regressor의 평면은 $\alpha_1 x_1 + \dotsb + \alpha_k x_k$ 와 같은 형태의 선형 결합을 통해 달성된다. 즉, $\alpha_i$ 를 어떻게 잡는지에 따라서 $k$ 차원까지 이 식을 통해서 생성할 수 있다. 그런데 $\overline{\mathbf Y}$ 는 1차원 즉, 모든 원소가 $\overline{y}$ , 즉 $y$ 의 평균이다. 따라서 이를 만족하는 $\alpha_i$ (for $i = 1, \dotsc, k$ )를 ${\rm col}~{\mathbf X}$ 에서 반드시 찾을 수 있다. ↩︎
궁여지책으로 이와 유사한 지표를 만들어낼 수는 있겠다. 여기를 참고하라. ↩︎
더 자세한 내용은 여기를 참고하자. ↩︎