Introduction
In online and mobile games based on a freemium model, the most commonly tracked metrics that constitute revenue are ARPPU (Average Revenue Per Paying User) and PU (Paying User). These two metrics play a crucial role in assessing the profitability of a game. However, these indicators are often analyzed and interpreted individually. Is there a more precise way to analyze these metrics together?
This article will explore a method to decompose revenue fluctuations into changes in these two constituent metrics.
Formula for Decomposing the Change of Sales
Notation
For \(t=1, 2, \dotsc\), we denote the following:
- \(y_t\): Revenue in period \(t\)
- \(a_t\): ARPPU in period \(t\)
- \(u_t\): PU in period \(t\)
The revenue in period \(t\) is given by \(y_{t}= a_t u_t\).
For \(t=2, 3, \dotsc\), the changes in each variable are as follows:
- Change in revenue in period \(t\): \(\Delta y_t = y_{t} - y_{t-1}\)
- Change in ARPPU in period \(t\): \(\Delta a_t = a_{t} - a_{t-1}\)
- Change in PU in period \(t\): \(\Delta u_t = u_{t} - u_{t-1}\)
And, the rates of change for each variable in period \(t\) are denoted as follows:
- Rate of change in revenue: \(\delta y(t) = \dfrac{\Delta y_{t}}{y_{t-1}}\)
- Rate of change in ARPPU: \(\delta a(t) = \dfrac{\Delta a_{t}}{a_{t-1}}\)
- Rate of change in PU: \(\delta u(t) = \dfrac{\Delta u_{t}}{u_{t-1}}\)
Decomposition by the change of ARPPU and PU
\[\begin{align*} \delta y(t) & = \dfrac{a_{t}u_{t} - a_{t-1} u_{t-1}}{y_{t-1}} \\ & = \dfrac{a_{t}u_{t} - a_{t-1} u_{t-1} + \overbrace{a_{t-1} u_{t} - a_{t-1} u_{t}}^{(*)}}{y_{t-1}} \\ & = \dfrac{a_{t}-a_{t-1}}{y_{t-1}} u_{t} + \dfrac{u_{t}-u_{t-1}}{y_{t-1}} a_{t-1} \\ & = \dfrac{a_{t}-a_{t-1}}{a_{t-1} u_{t-1}} u_{t} + \dfrac{u_{t}-u_{t-1}}{a_{t-1} u_{t-1}} a_{t-1} \\ & = \delta a(t) \dfrac{u_{t}}{u_{t-1}} + \delta u(t) \end{align*}\]
By substituting \((*)\) with \((u_{t-1} a_{t} - u_{t-1} a_t)\) in the above equations, we can derive the following:
\[\begin{align*} \delta y_{t} = \delta u(t) \dfrac{a_{t}}{a_{t-1}} + \delta a_{t} \end{align*}\]
Now, by adding the two equations that express \(\delta y(t)\), we obtain the following:
\[\begin{align*} 2\delta y(t) &= \delta a(t) (\dfrac{u_{t}}{u_{t-1}}+1) + \delta u(t)(\dfrac{a_{t}}{a_{t-1}} + 1) \\ \delta y(t) &= c_a \cdot \delta a(t) + c_u \cdot \delta u(t) \end{align*}\]
where
\[\begin{align*} c_a &= \dfrac{1}{2}\left( \dfrac{u_t}{u_{t-1}} + 1 \right) \\ c_u &= \dfrac{1}{2}\left( \dfrac{a_t}{a_{t-1}} + 1 \right) \end{align*}\]
Short interpretation
As observed from the equation, the rate of change in revenue is the sum of the products of the rate of change of the two metrics and their respective adjustment factors. In other words, the rate of change in revenue can be decomposed into the contribution from changes in ARPPU and the contribution from changes in PU.
Let’s examine the adjustment factors. If the PU in the current period has increased compared to the previous period, then \(c_u > 1\). Similarly, if the ARPPU has increased, then \(c_a > 1\). When these factors are greater than 1, it indicates that the impact of changes in \(\delta a(t)\) or \(\delta u(t)\) is amplified.
This interpretation is intuitive. If the ARPPU in the previous period has increased, it becomes more crucial to increase PU in the current period. Conversely, if PU has increased, then increasing ARPPU becomes more important.
Practical Applications
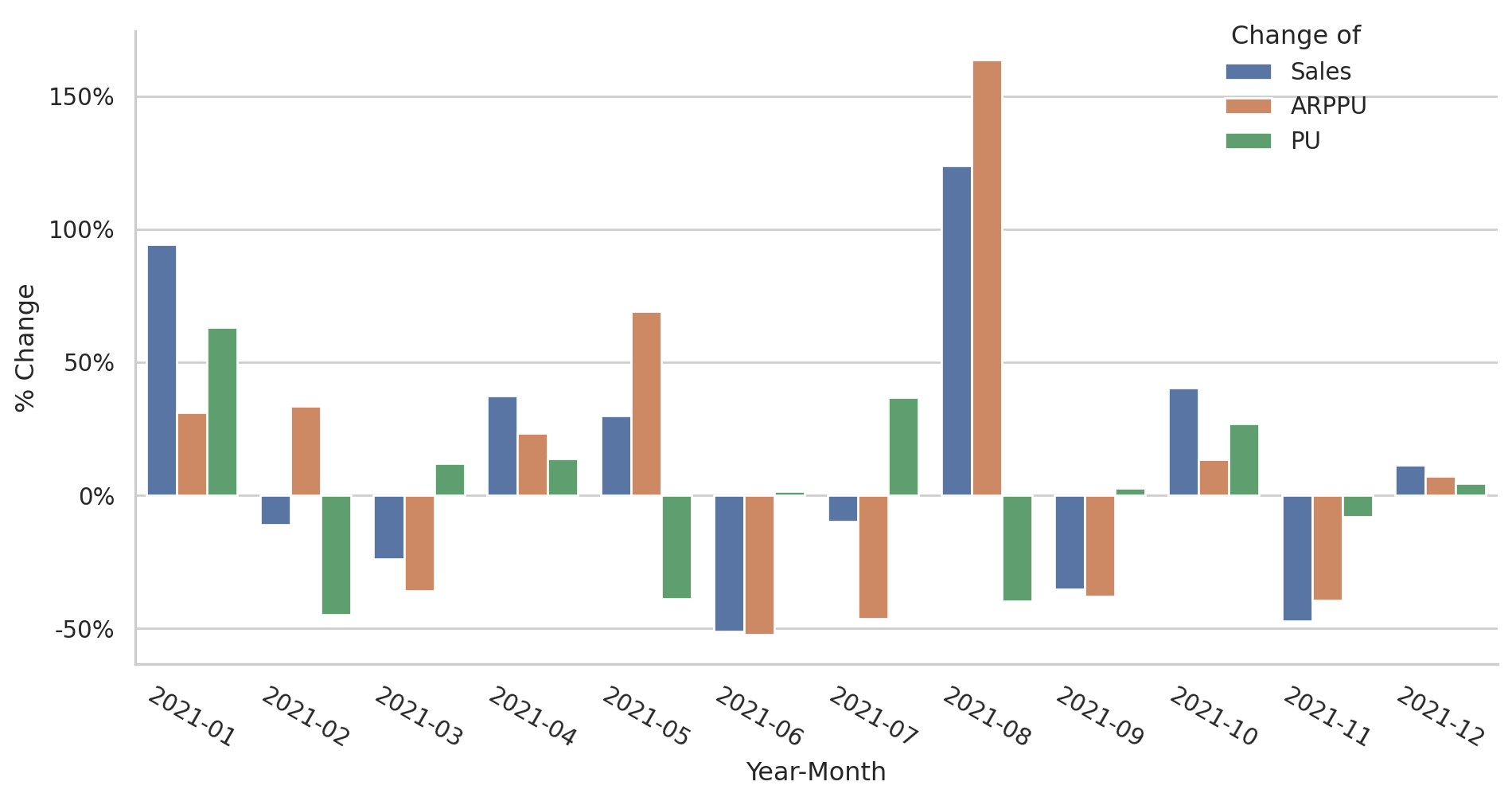
Figure 1 illustrates the decomposition of revenue changes into the contributions from changes in ARPPU and PU using artificially generated monthly revenue data over one year.1 Consider July 2021. The slight decrease in revenue is the result of significant movements in ARPPU and PU in opposite directions. By analyzing it this way, we can observe not only the changes in revenue itself but also the direction of the monetization strategy within the game.
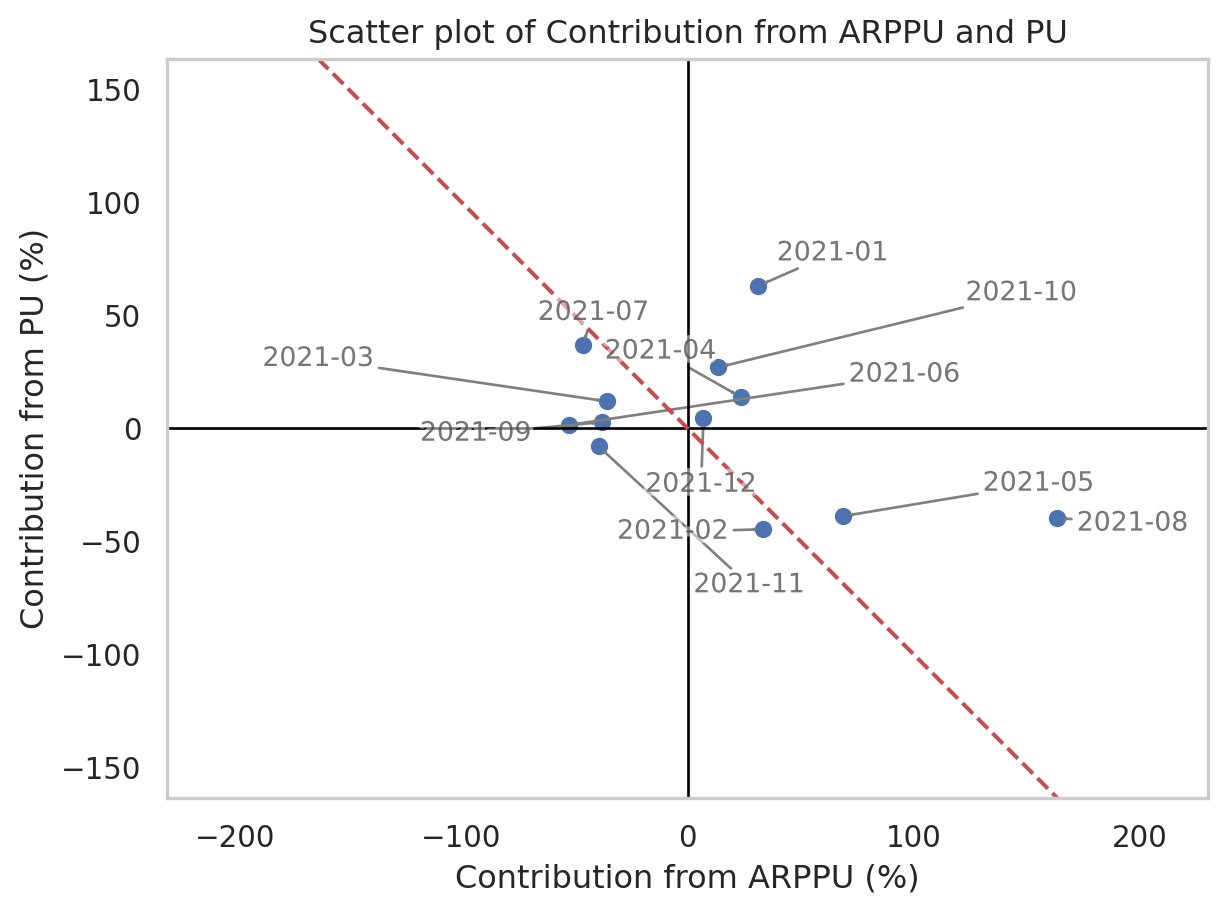
Next, let’s represent the contributions of changes in ARPPU and PU as scatter plots for each month. Specifically, we will plot \(c_u \cdot \delta a(t)\) and \(c_a \cdot \delta u(t)\) on the \(x\) and \(y\) axes, respectively, for each period \(t\). This will allow us to assess the effectiveness of the revenue strategies employed during the respective periods. By doing so, we can distinguish and examine the impact of changes in ARPPU and PU on revenue fluctuations.
Figure 2 depicts the contributions of changes in ARPPU and PU as a scatter plot based on our simulated data. The upper half of the plot represents areas where revenue has increased, while the lower half represents areas where revenue has decreased.
Through this visualization, one can quantitatively assess whether the intended revenue strategies for the game were achieved. For instance, consider February 2021. If the revenue expansion strategy for February was to increase PU, then this objective was accomplished. However, the decrease in ARPPU resulted in a larger reduction in revenue, leading to a slight overall decrease in revenue. In this way, the scatter plot allows for a clear, post hoc evaluation of whether the strategies employed for a particular month achieved their targets.
Footnotes
Unfortunately, I cannot open a real data set due to confidentiality issues. However, the data used in this article is generated in a way that reflects the characteristics of real data and can be used for explantory purposes.↩︎