당연히 알고 있다고 생각하지만 모르는 게 생각보다 많다. 회귀 분석에서 로그-리니어 모델, 즉 종속 변수에 로그를 취하고 독립 변수가 선형인 모델을 어떻게 이해해야 할까? 찬찬히 따져보자.

The Math

편의상 독립 변수와 종속 변수 모두 스칼라 값이라고 하자.

$$ \ln y_i = \beta x_i + \varepsilon_i $$

양변을 미분해보자. 오차항은 정의상 $x_i$와 무관해야 하므로,

$$ \dfrac{d y_i}{y_i} = \beta d x_i $$
$$ \dfrac{d y_i / y_i}{d x_i} = \beta $$

이렇게 보면 $\beta$ 값은 $x_i$가 순간적으로 변함에 따라서 변화하는 $y_i$의 % 변화를 나타낸다. 일단 기본적으로 주의해야 할 것! 위 값은 국지적 미분 값이다. 즉, 특정한 $x_i$에서의 미분 값이다. 즉, 엄밀하게 쓰면,

$$ \dfrac{d y_i / y_i}{d x_i} \bigg|_{x_i = x_0} = \beta $$

회귀분석에서 구하는 $\beta$와 의 위 식에서 얻는 $\beta$는 동일할 수가 없다. 왜나하면, $y_i$는 지수 함수라는 비선형 함수이기 때문이다. 일단 이 점을 기억해두도록 하자.

The Coefficient

회귀 분석으로 돌아오자. 독립 변수 $y_i$에 $\ln$을 취해서 변형을 취했다. 그 의미를 풀어보자.

$$ \begin{aligned} \Delta \ln y_i & = \ln y_1 - \ln y_0 \\ & = \ln(\frac{y_1}{y_0}) \\ & = \ln(\frac{y_0 + \Delta y}{y_0}) \\ & = \ln(1+\frac{\Delta y}{y_0}) \end{aligned} $$

$\ln(1+\frac{\Delta y}{y_0})$를 보자. $z=0$ 근처에서 $\ln (1+z) \approx z$가 성립한다.1

$$ \Delta \ln y_i = \ln(1+\frac{\Delta y}{y_0}) \approx \dfrac{\Delta y}{y_0} = \% \Delta y = \beta \Delta x $$

이 경우 수학적인 해석을 거의 그대로 가져올 수 있다. 다만, $\frac{\Delta y}{y_0}$가 0 근처에 있어야 한다. 이는 $y$의 변화율이 크지 않은 경우에 해당한다.

위와 같은 회귀식을 추정해 $\beta$를 보고할 때 “$x$가 1단위 변화할 때”라는 표현을 쓴다. 즉, $\Delta x = 1$로 둔다는 뜻이다.

$$ \Delta \ln y_i \approx \dfrac{\Delta y}{y_0} = \% \Delta y = \beta $$

결국 $\beta$의 값이 0 주변에 있다면 이 값은 $x_i$가 1단위 변화할 때 $y_i$의 변화율에 미치는 영향”으로 해석할 수 있다.

Exact Math for the Percent Change

근사값을 쓰지 말고 % 변화율을 정확하게 계산해보자. 물론 이 값이 필요한 경우에 해당한다.

$$ \begin{aligned} \% \Delta y_i & \equiv \dfrac{y_1 - y_0}{y_0} \\ & = \dfrac{y_1}{y_0} - 1 \\ & = \exp(\ln (\dfrac{y_1}{y_0})) - 1 \\ & = \exp(x_1 \beta - x_0 \beta + \varepsilon_1 - \varepsilon_0) - 1 \\ & = \exp(\Delta x \beta + \Delta \varepsilon) - 1 \end{aligned} $$

$\Delta \varepsilon =0$를 가정하고 $\Delta x =1$로 두면, 위 식으로 $y_i$의 % 변화율을 계산할 수 있다.

Interpretation

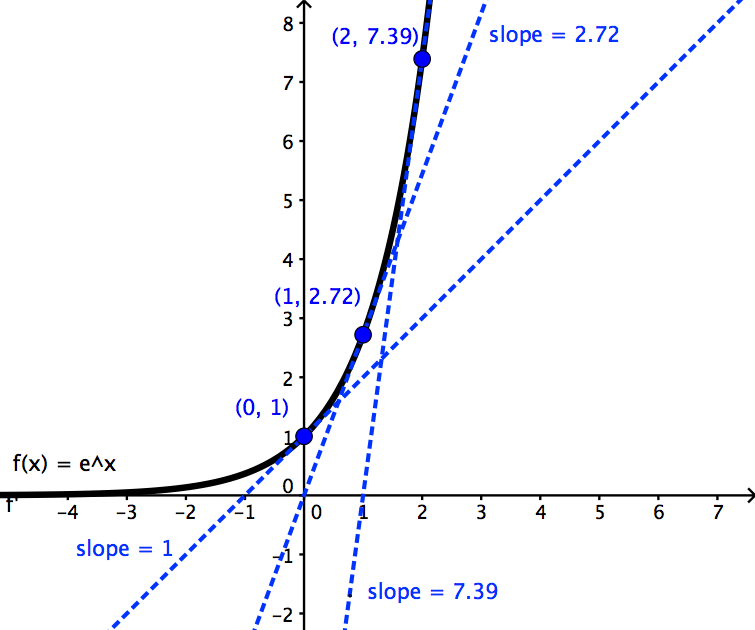
위 지수 함수의 그림을 보자. $x$가 커짐에 따라서 도함수의 기울기가 커진다는 점을 알 수 있다. 특정 $x$ 구역에서 회귀 계수를 구하면 이 도함수의 기울기와 비슷해질 것이고, 이는 이 도함수를 기울기로 근사한 직선이 실제 $y_i$값 보다는 작게 될 것이다. 즉, 변화율 측정 단위로서 $\beta$는 실제 변화율보다 작게 된다.

만일 $\beta = 0.3$이라고 하자. 실제 $\%\Delta y$를 구해보면,

$$ \%\Delta y = \exp(\beta) - 1 = 0.35 $$

약 5% 정도 과소 평가 되었음을 알 수 있다. 이 크기의 의미나 중요성은 분석자가 선택할 문제다.

  1. $z=0$ 근방에서 테일러 급수를 1차까지 근사하면 저 값을 얻을 수 있다. $z=0$ 인근에서 근사하는 이유는 $z=0$ 근처에서 $\frac{(z-0)^k}{k!}$ for $k=2,3,\dotsc$과 같은 고차 항의 크기가 점점 줄어들기 때문이다. ↩