Why Radian
360$\degree$ 도법은 익숙하지만 다소 자의적이다. 사실 호도법을 도입하는 이유는 $\pi$를 계산에 통합하기 위해서가 아닐까? 호도법으로 표기하면 미분 등을 할 때 $\pi$가 튀어나오지 않는다.
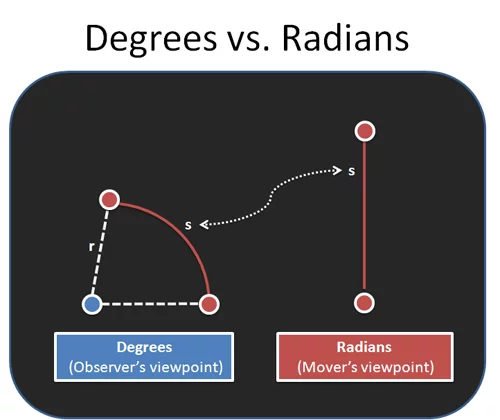
그림에서 보듯 각도법은 중심에 위치한 관찰자의 위치를 반영한다. 반면 호도법은 반지름 대비 원주 상에서 이동한 거리로 각을 표시한다. 호도법으로 각도를 나타내는 법은 다음과 같다.
$$
\theta = \dfrac{s}{r}
$$
- $\theta$: 각도
- $s$: 원주에서 이동한 거리
- $r$: 반지름
Circumvent of Circle
$d\degree$의 각도를 지니는 호의 길이를 구해보자.
$$
r (2 \pi) \dfrac{d\degree}{360 \degree}
$$
이를 호도법으로 나타나면 다음과 같다. 우선 각도를 호로 바꿔야 한다. $\frac{d\degree}{360 \degree}$ 부분을 호도법으로 바꿔야 한다. 따라서 분자와 분모 모두를 호도로 고쳐보자.
$$
360 \degree = \dfrac{r (2\pi)}{r} \rm radian = 2 \pi ~\rm radian
$$
$d\degree = \theta~\rm radian$이므로,라고 하자.
$$
r (2\pi) \dfrac{\theta}{2 \pi} = r \theta
$$
즉 호도법으로 원호의 길이는 $r \theta$로 간편하게 표기된다. 호의 면적 역시 마찬가지다.
$$
r^2 \pi \dfrac{\theta}{2 \pi} = r^2 \dfrac{\theta}{2}
$$
Limit of sin, cos
Limit of sin

삼각형의 면적을 보자.
$$
\begin{aligned}
\triangle {\rm OAI} & = \dfrac{1}{2} {\rm height} \cdot \overline{\rm OI} = \dfrac{1}{2}\sin \theta \cdot 1 \\
\frown{\rm OAB} &= \dfrac{1}{2} 1^2 \theta \\
\triangle {\rm OTI} &= \dfrac{1}{2}\overline{\rm TI} \cdot \overline{\rm OI} = \dfrac{1}{2}1\cdot \tan \theta
\end{aligned}
$$
이 사이에 아래와 같은 관계가 성립한다.
$$
\triangle \rm OAB \leq \frown \rm OAB \leq \triangle \rm OAC
$$
$$
\sin \theta \leq \theta \leq \tan \theta
$$
$$
\dfrac{\sin \theta}{\sin \theta} \leq \dfrac{\theta}{\sin \theta} \leq \dfrac{\tan \theta}{\sin \theta}
$$
$$
1 \geq \dfrac{\sin \theta}{\theta} \geq {\cos \theta}
$$
$$
1 \geq \lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} \geq \lim_{\theta \to 0} \cos \theta (= 1)
$$
샌드위치 정리에 따라서 $\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta} =1$.
Limit of cos
$$
\lim_{\theta \to 0} \dfrac{\cos \theta -1}{\theta}
$$
$$
\begin{aligned}
\dfrac{\cos \theta -1}{\theta} \cdot \dfrac{\cos \theta + 1}{\cos \theta +1} &= \dfrac{\cos^2 \theta - 1}{\theta(\cos \theta +1)} \\
&= \dfrac{-\sin^2 \theta}{\theta(\cos \theta + 1)} \\
& = \dfrac{-\sin \theta}{\theta} \dfrac{\sin \theta}{\cos \theta + 1}
\end{aligned}
$$
$$
\lim_{\theta \to 0} \dfrac{\cos \theta -1}{\theta} = (-1) \cdot 0 = 0
$$
Derivative of Sin
정의를 그대로 활용하면 된다.
$$
\begin{aligned}
\dfrac{d}{d \theta} \sin \theta & = \lim_{\delta \to 0} \dfrac{\sin (\theta+\delta) - \sin \theta }{\delta} \\
& = \lim_{\delta \to 0} \dfrac{\sin \theta \cos \delta +\sin \delta \cos \theta - \sin \theta }{\delta} \\
& = \cos \theta \lim_{\delta \to 0} \dfrac{\sin \delta}{\delta} \\
& = \cos \theta
\end{aligned}
$$
$$
\begin{aligned}
\dfrac{d}{d \theta} \cos \theta & = \lim_{\delta \to 0} \dfrac{\cos (\theta+\delta) - \cos \theta }{\delta} \\
& = \lim_{\delta \to 0} \dfrac{\cos \theta \cos \delta -\sin \delta \sin \theta - \cos \theta }{\delta} \\
& = \lim_{\delta \to 0}\dfrac{\cos \theta(\cos \delta -1)-\sin\delta \sin\theta}{\delta} \\
& = 0 - (1) \sin \theta \\
& = - \sin \theta
\end{aligned}
$$
Taylor Series for sin, cos
이제 $\sin \theta$, $\cos \theta$를 $\theta$로 0 근방에서 전개해보자.
$$
\begin{aligned}
\sin \theta & = \sin 0 + \sin' 0(\theta - 0) + \dfrac{\sin'' 0}{2!}(\theta - 0)^2 + \dfrac{\sin''' 0}{3!}(\theta - 0)^3 + \dotsb \\
& = 0 + \theta + \dfrac{(-1)}{3!} \theta^3 + \dotsb \\
& = \theta - \dfrac{1}{3!} \theta^3 + \dfrac{1}{5!} \theta^5 -\dotsb
\end{aligned}
$$
$$
\begin{aligned}
\cos \theta & = \cos 0 + \cos' 0(\theta - 0) + \dfrac{\cos'' 0}{2!}(\theta - 0)^2 + \dfrac{\cos''' 0}{3!}(\theta - 0)^3 + \dotsb \\
& = 1 + (-\sin 0)\theta + \dfrac{(-\cos\theta)}{2!} \theta^2 + \dotsb \\
& = 1 - \dfrac{1}{2!} \theta^2 + \dfrac{1}{4!} \theta^4 - \dotsb
\end{aligned}
$$
Taylor Series $e^{i \theta}$
$$
\begin{aligned}
e^{i \theta} &= e^0 + i (\theta - 0) + \dfrac{(i)^2}{2} (\theta-0)^2 + \dotsb \\
& = 1 + i \theta - \dfrac{\theta^2}{2!} - i \dfrac{\theta^3}{3!} + \dfrac{\theta^4}{4!} + i \dfrac{\theta^5}{5!}
\end{aligned}
$$
실수와 허수를 따로 모아주면,
$$
\begin{aligned}
e^{i \theta} & = (1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} - \dotsb) + (\theta - \dfrac{\theta^3}{3!} + \dfrac{\theta^5}{5!} - \dotsb)i \\
& = \cos \theta + i \cdot \sin \theta
\end{aligned}
$$
Polar Representation
허수를 나타내는 가장 신박한 방법일지 모르겠다.
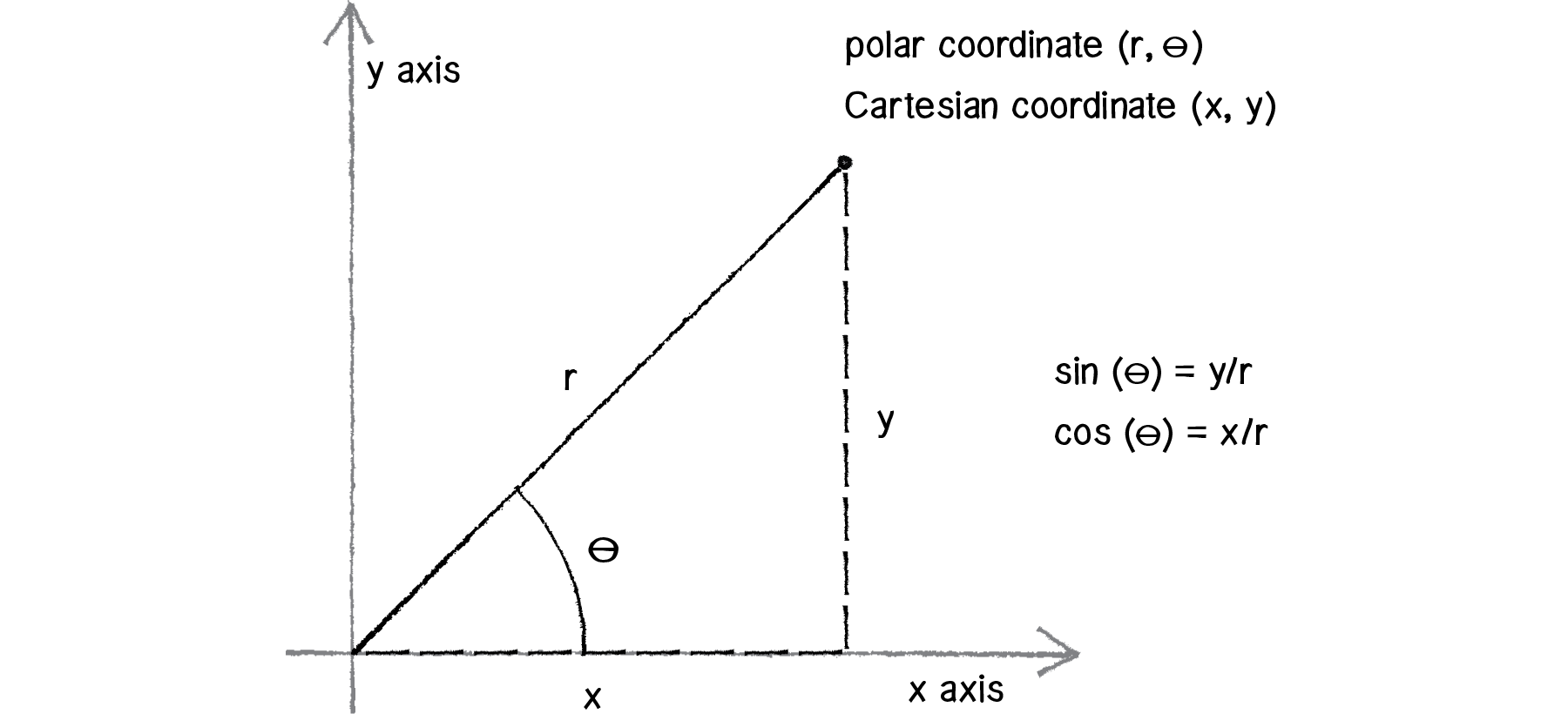
허수를 $x-y$로 구성된 데카르트 평면에 표시한다고 하자. 이때, 일반적으로 $x + i y$는 위의 그림과 같이 표시된다. 이를 극좌표(polar coordinate)로 나타내는 방법은 원점에서 해당 벡터까지의 ‘거리’와 x축의 양의 방향을 0도의 기준으로 잡은 ‘각도’로 다시 표기하는 것이다. 즉,
$$
z = x + yi = |z| \angle{\theta} = \underbrace{|z| \cos \theta}_{x} + \underbrace{|z| \sin\theta}_{y} i
$$
$r = \sqrt{x^2 + y^2}$가 데카르트 좌표 위에서 표현하는 위치까지의 거리를 스케일링하는데, 이는 원의 반지름과 같은 의미가 된다. 원 위에서의 위치는 $\theta$로 나타낼 수 있다.
앞서 본 결과는 다음과 같다.
$$
e^{\theta i} = \sin\theta + i \cdot \cos \theta
$$
$\theta$는 각이기 때문에 이 녀석을 $\pi$만큼 돌려보도록 하자. 그러면 데카르트 좌표에서 $(-1,0)$에 떨어진다. 이는 실수-허수 평면에서 실수 $-1$, 허수 $0$이다. 즉,
$$
e^{\pi i} + 1 = 0
$$
이 항등식은 수학의 역사에서 가장 중요한 다섯 개의 숫자($e, \pi, i, 0, 1$) 사이의 관계를 나타낸다.
De Moivre’s law
이런 관점에서 보면 드무아브르의 법칙 역시 자명하다.
$$
e^{\theta i} = \sin\theta + i \cdot \cos\theta
$$
$$
(e^{\theta i})^n = e^{n\theta i} = \sin n \theta + i \cdot \cos n \theta
$$
$e^{\theta i}$의 $n$ 승이 단위원을 중심으로 $n \theta$ 만큼 회전 이동한 (각의 크기가 바뀐) 값을 지니게 된다는 사실을 쉽게 알 수 있다.
Some Exercises
위의 사실들을 활용하면 몇 가지 재미있는 계산을 할 수 있다.
$$
e^i = \sin 1 + i \cdot \cos 1
$$
$3^i$는 어떨까? 이상해보이는 숫자지만, $e$를 활용하면 된다.
$$
(e^{\ln 3})^i = \sin \ln 3 + i \cdot \cos \ln 3
$$
$i^i$는 어떨까? $i = e^{\frac{\pi}{2} i}$이다. 원 (1,0), 즉 $e^{0+0i}$에서 90도 각을 지니면 좌표에서 $i$에 도달하게 된다.
$$
i^i = (e^{\frac{\pi}{2} i})^i = e^{-\frac{\pi}{2}}
$$
$\ln i$도 자연스럽게 구할 수 있다. 먼저 위의 식에서 $\ln i^i = - \dfrac{\pi}{2}$를 알 수 있다. 그리고
$$
\ln i^i = i \ln i = -\dfrac{\pi}{2}
$$
양변에 $i$를 곱하면, $\ln i = \dfrac{\pi}{2} i$.
Complex growth
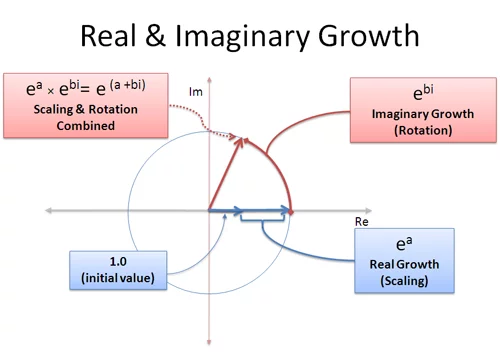
$e^x$에서 $x$가 각각 실수부와 허수부일 때 해당 부분은 실수 증가와 회전으로 나누어 볼 수 있다. 즉 데카르트 좌표에서 극 좌표를 찾는 과정으로 위의 그림과 같다. 이 말을 좀 더 자세히 살펴보자.
임의의 허수 $6 + 8i$가 있다고 하자. 이 허수를 나타내는 $e^{a+bi}$를 찾을 수 있다는 의미이기도 하다.
- 먼저 길이를 찾는다. $\sqrt{6^2 + 8^2} = 10$. 이제 $b=0$으로 두고 $a$를 먼저 찾는다. $e^a = 10$에서 양변에 $\ln$을 취해주면 된다.
- $\cos \theta = \frac{6}{10}$, $\sin \theta = \frac{8}{10}$을 통해 각도 $\theta$를 구할 수 있다.
- $\ln 10 \approx 2.3$, $\theta \approx 0.93$라도 두면 $6 + 8i \approx e^{2.3 + 0.93 i}$로 나타낼 수 있다.



